4.5. Méthode des Ellipses
et discussion de la précision 4.5. Méthode des Ellipses
et discussion de la précision
4.5.2. Inversion des variables
4.5.4. Précision des paramètres obtenus
début
En n'utilisant, ici, que les incertitudes sur les 
et sur les 
,
on obtient:
et 
avec 
et
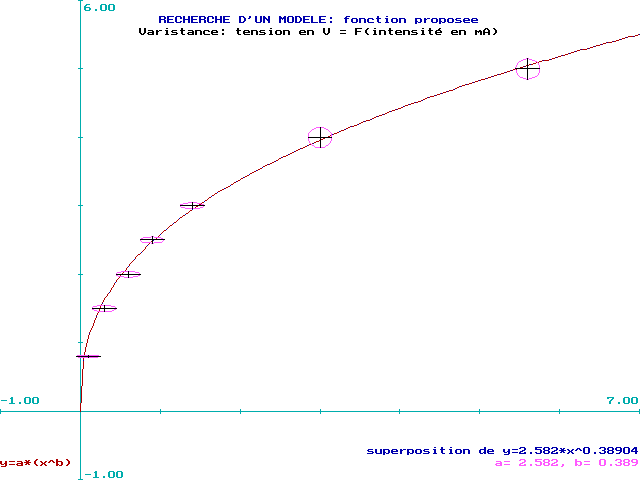
Sur la figure 9 , la courbe semble passer "au mieux" dans les ellipses de dispersion unitaires, ce qui est fort discutable ! Il reste, cependant, le problème de l'évaluation des résultats obtenus.
On peut vérifier, toutefois, que la présence ou non du premier point litigieux influe peu sur l'estimation des paramètres (écarts relatifs inférieurs à cinq pour mille avec une légère augmentation du CRITERE de l'ordre de deux pour cent) , ce qui n'est pas le cas avec les autres méthodes.
Figure 9: Méthode des
Ellipses
début
D'autre part, soulignons que les difficultés rencontrées dans
l'exemple étudié découlent de ce que l'expérimentateur
a choisi d'étudier la caractéristique
intensité-tension, soit:
Il pouvait s'intéresser à la caractéristique tension-intensité,
la forme de la loi restant la même:
avec
et 
.
Dans cette nouvelle situation, les incertitudes sur la variable expliquée I sont d'écart-type constant, alors que celles sur la variable explicative U sont négligeables pour les faibles valeurs de U et sans grande influence pour les autres.
Dans ce cas, sauf pour l'utilisation de l'Anamorphose, les résultats de l'optimisation dépendent peu de la méthode suivie et on retrouve, aux arrondis près, les valeurs de la Méthode des Ellipses pour l'autre représentation.
Ainsi, par la Méthode des Moindres Carrés, les évaluations de la résistance R ou de la conductance G d'un résistor linéaire, ne sont pas exactement compatibles puisque les variables U et I jouent des rôles non symétriques.
On retiendra que le choix de la forme de la fonction à vérifier, doit respecter au mieux les hypothèses sous-entendues par la méthode d'optimisation utilisée.
début
Elle est très inférieure à 1 , ce qui, théoriquement, est peu probable, ainsi que le passage systématique de la courbe à l'intérieur des Ellipses de Dispersion Unitaires (phénomènes liés...) .
En fait, une meilleure évaluation des écart-types
sur les et les ,
est obtenue en divisant par 2,5 à 3 les valeurs déduites de la
classe de l'appareil.
On obtient alors un CRITERE de l'ordre de:
sur
une variable,
ce qui est beaucoup plus cohérent et exploitable.
Ainsi, en se reportant à l'exemple
1 (pour 
) ,
on estime que seules les Méthodes du Modèle et des Ellipses paraissent
acceptables.
Cela résout aussi le problème de la dispersion insuffisante des mesures comme le montre la figure 10 (à comparer à la figure 1 ) et les figures 11 et 12 qui représentent la dispersion relative des points expérimentaux par rapport aux "points les plus probables" de la courbe optimisée par ces deux méthodes.
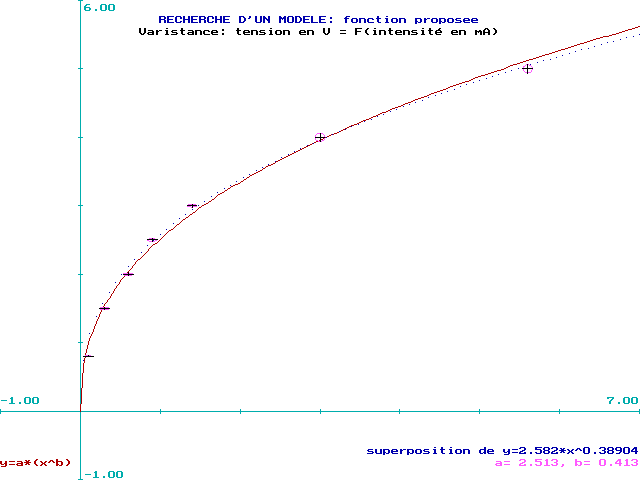
Figure 11: Méthode
du Modèle
Figure 12: Méthode des
Ellipses
4.5.4. Précision des paramètres
obtenus
début
Le Logiciel ACTILAB donne les résultats numériques bruts sous la forme:
sur
une variable:
Une discussion détaillée s'impose, car les résultats les plus précis semblent être obtenus par la méthode donnant le plus mauvais ajustement !
Remarque: Le non recouvrement des domaines d'incertitude, ne constitue pas nécessairement une "catastrophe", quand on se souvient que l'incertitude numérique devrait être représentée par l'écart-type et que la probabilité de s'écarter de plus d'un écart-type est relativement importante (cf. la discussion précédente) . Cependant, le phénomène est amplifié si l'on tient compte des écart-types corrigés (c.a.d. divisés par 2,5 à 3 ) .
Ainsi, la comparaison des courbes isocritères
(à 
)
par la Méthode du Modèle et par la Méthode des Ellipses
est plus instructive (cf. figures 13 et 14 ) .
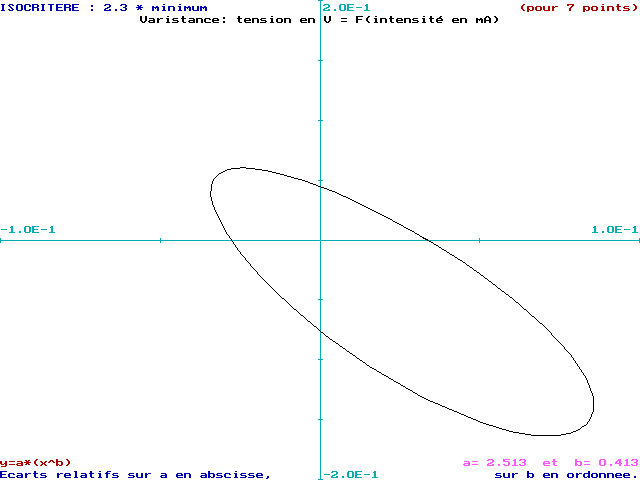
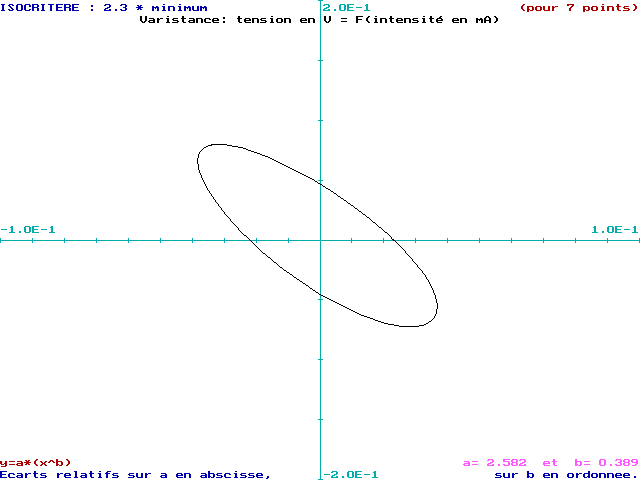
On observe un "décalage" de la courbe obtenue par la Méthode
du Modèle. On rappelle que la "métrique" utilisée
ici, est celle déduite du généralisé
et que la mise en évidence du biais disparaît si on se limite au
Critère Quadratique.
Cela sous-entend que l'on considère que le est,
a priori, le plus représentatif, ce qui est, bien sûr, discutable !
On remarque, aussi, que l'extension de la courbe isocritère de la Méthode des Ellipses est légèrement plus faible, ce qui peut s'interpréter par le fait que la détermination des paramètres serait plus précise.
Les défauts constatés sont accentués par la Méthode
du sur une seule
variable comme on pourra le vérifier sur la courbe isocritère
de l'exemple 3 précédent.
4.5.5. Discussion finale
début
Cependant, même dans le cas le plus favorable, les écarts relatifs restent importants:
de l'ordre de 4% pour a et de 8% pour b
(valeurs cohérentes avec les conclusions d'ACTILAB pour la Méthode des Ellipses) .
De tels résultats doivent alerter l'expérimentateur.
De plus, une observation attentive des courbes représentant la fonction étudiée, permet de détecter dans la distribution des points expérimentaux, une courbure régulière non prise en compte complètement par le Modèle proposé. En effet, encore une fois, les écarts constatés devraient avoir un caractère aléatoire et ,donc, non ordonné.
En fait, ce manque de cohérence pourrait être attribué à deux raisons principales:
On constate, encore une fois, que la perfection expérimentale n'existe
pas et qu'une modélisation ne coïncide jamais parfaitement avec
la réalité ...
Titre, résumé
retour: Varistance Sommaire
suite: Conclusion
