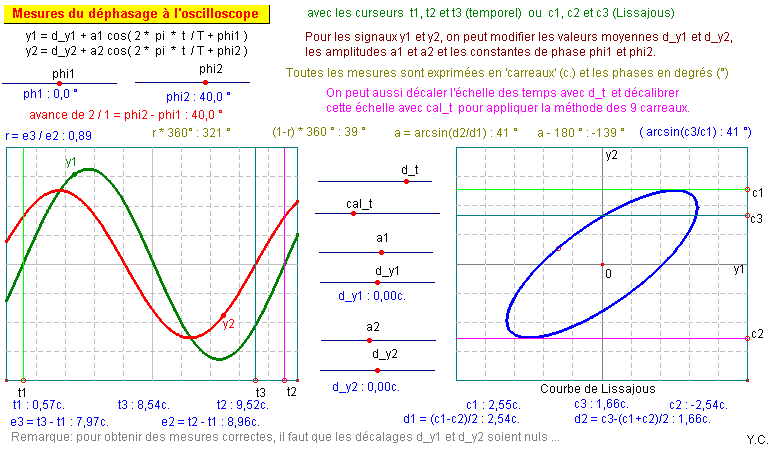
Méthode des neuf carreaux :
- régler les décalages verticaux de manière
que les moyennes de y1 et y2 correspondent à l'axe horizontal.
- choisir la trace de référence (y1 ou y2) et placer
son origine à gauche de l'écran avec le paramètre
d_t :
ceci correspond à modifier le décalage en temps
de l'oscilloscope.
- déterminer a priori quelle est la nature du
déphasage (avance ou retard) du 2ème
signal par rapport au 1er.
- décalibrer l'échelle de temps avec cal_t
de façon à ce que la période
corresponde à 9 carreaux ;
il sera peut-être nécessaire de rerégler
l'origine des temps simultanément.
- entre 2 passages à 0 dans le même sens pour
y1 et y2, évaluer l'écart de phase en carreaux
cette évaluation devrait pouvoir se faire au quart de carreau
près pour des amplitudes a1 et a2 assez grandes.
- pour obtenir le déphasage en degrés, multiplier
ce nombre de carreaux par 40 (360° / 9 = 40°).
Le déphasage obtenu devrait correspondre à la valeur
affichée à mieux que 10 ° près !
Remarque: on peut aussi régler la demi-période
à 9 carreaux, ce qui double la précision de
la mesure...
(le nombre de carreaux de l'écart de phase doit être alors
multiplié par 20 car 180° / 9 = 20°)
Utilisation des curseurs t1, t2 et t3 :
Le principe est identique mais l'évaluation de la période
e2 = t2 - t1 correspond à un nombre quelconque de carreaux.
L'écart e3 = t3 - t1 correspond à l'écart
de phase en temps et le rapport r = e3 / e2 s'exprime en fraction
de période.
La multiplication de r par 360° permet d'obtenir le déphasage
en degrés ...
Remarque: ici aussi, pour améliorer la précision,
on peut prendre pour référence la demi-période,
soit 180°
Utilisation de la courbe de Lissajous :
Les curseurs c1 et c2 positionnés sur les extremums
de l'ellipse permettent d'évaluer l'amplitude d2 = (c1-c2)/2
de y2.
Le curseur c3 correspond à l'intersection supérieure
de cette ellipse avec l'axe vertical.
Il permet de calculer d3 = c3-(c1+c2)/2 , sa position par rapport
au centre de symétrie de l'ellipse.
Puis le calcul de d3/d2 donne la valeur absolue du sinus de
l'écart de phase recherché.
Dans le cas d'une ellipse parfaitement centrée, on peut
utiliser plus simplement c3/c1 à la place de d3/d2.
Remarque:
cette méthode ne permet pas d'obtenir le signe du déphasage
à moins de connaître le sens de parcours sur l'ellipse.
|