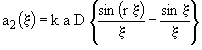4. Cas particulier :

cf. exercice P-21.5 de Pérez, Optique (Masson) , p. 235

4.1. Enoncé :                   

On limitera les calculs aux cas des fentes extrêmement longues et pas trop larges pour pouvoir négliger la diffraction correspondant à la longueur mais pas celle correspondant à la largeur.

Dans ce cadre, on prendra donc :

·  pupille P : fente de largeur L telle que t(x) = 1 pour et t(x) = 0 ailleurs ;

·  pupille P₁ : fente de largeur a telle que t(x) = 1 pour et t(x) = 0 ailleurs ;

·  pupille P₂ : deux fentes de largeur telle que t(x) = 1 pour et t(x) = 0 ailleurs ;

Les pupilles P₁ et P₂ sont bien complémentaires pour la pupille P :

On prendra où l est la longueur d’onde.

Remarque :  on fait des hypothèses de même type pour l’exercice classique décrivant la strioscopie proposé, par exemple, dans l’ouvrage de Lecardonnel et Tilloy , Optique (Bréal) , p. 146 .

4.2. Calcul de l’intensité :                   

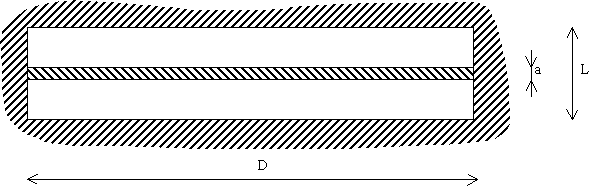
En appliquant le principe d’Huygens-Fresnel, pour une fente élémentaire de coordonnée x , de largeur dx et de longueur D , dans la direction q par rapport à Oz dans le plan Oxz :

amplitude complexe : à sommer sur la totalité de la pupille.

·  pour la pupille P (fente de largeur L ) :

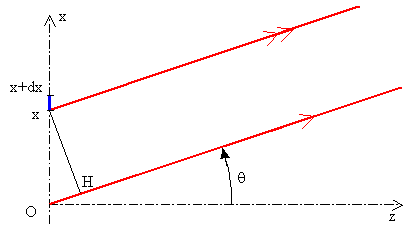
·  pour la pupille P₁ (fente de largeur a ) :

·  pour la pupille P₂ (complémentaire des précédentes) :

Il est intéressant d’introduire les paramètres :

et  

On obtient alors :

·  pour la pupille P :  

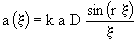
·  pour la pupille P₁ :  

·  pour la pupille P₂ :  

.

retour: Extension