5. Validité du théorème de Babinet :

5.1. Discussion qualitative :                   

Le théorème de Babinet sera applicable dans ce cas particulier si on peut négliger devant en dehors de l’image géométrique c’est à dire lorsque ou (très facile à réaliser car  ) .

On aurait alors comme prévu :

  et  

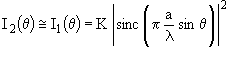
Cependant, cette condition n’est sûrement pas respectée pour les valeurs non nulles de x car les deux termes et sont du même ordre de grandeur .

5.2. Tracé des fonctions :                   

Pour faire une comparaison plus précise, on va tracer sur le même graphe les fonctions représentant les intensités relatives :

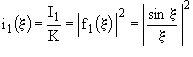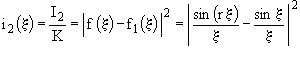et avec

Pour le tracé effectif, on prendra une valeur du paramètre r suffisamment grande pour respecter les hypothèses du problème, mais pas trop pour que les variations de soit encore visible.

En pratique on choisira r égal à quelques dizaines :

·  r = 10 :

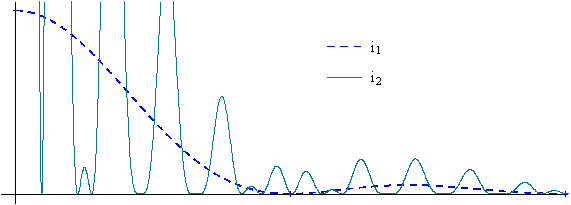
·  r =  30 :

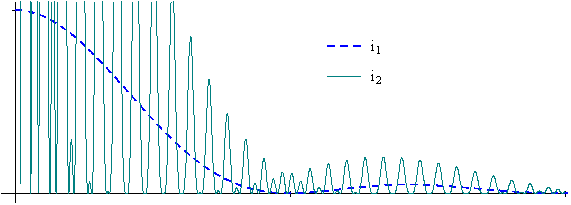
·  r = 50 :

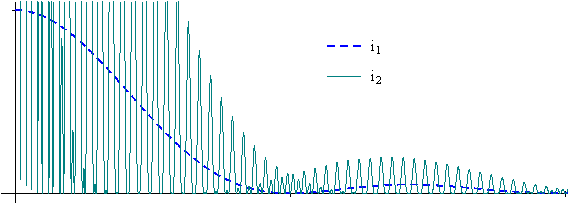
On constate, comme prévu précédemment, que l’augmentation de r ne permet pas d’identifier les deux fonctions !

 Simulation  avec Cabri Géomètre

.

retour: Cas particulier