7. Cas bidimensionnel :

7.1. Description :                   

On prendra pour pupille P₁ un disque de centre O et de rayon R₁ et pour pupille P un disque coplanaire de même centre et de rayon R₀ :

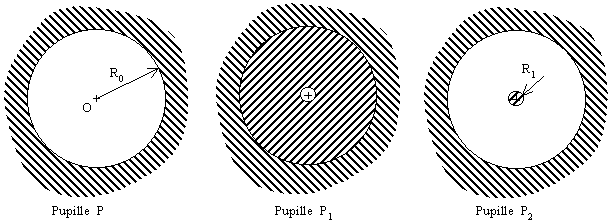
Les pupilles P₁ et P₂ sont bien complémentaires pour la pupille P .

On posera r = R₀ / R₁ ( r >> 1 a priori) .

7.2. Diffraction :                   

Pour une ouverture circulaire éclairée orthogonalement par une onde plane monochromatique, la diffraction de Fraunhofer fait intervenir la fonction de Bessel d’ordre 1 .

On obtient alors dans la direction faisant l’angle a avec la normale, les amplitudes complexes suivantes :

·  pour la pupille P₁ (disque de rayon R₁ ) :    avec

·  pour la pupille P (disque de rayon R₀ = r R₁ ) :  

·  pour la pupille P₂ (complémentaire des précédentes) :  

D’où les intensités correspondantes :

·  pour la pupille P₁ :  

·  pour la pupille P₂ :  

7.3. Discussion qualitative :                   

On sait qu’une fonction de Bessel se rapproche rapidement de son comportement asymptotique pour u grand selon :

d’ordre de grandeur typique

On constate alors que les deux termes qui interviennent dans a₂ sont d’ordre de grandeur :

·   provenant de a₁ ;

·   provenant de a ;

Comme r >> 1 , le terme prépondérant n’est pas celui espéré !

On obtiendra donc :  I₁ ¹  I₂ ... et le théorème de Babinet ne s’appliquera pas.

7.4. Observation :                   

L’œil ne pouvant détecter les variations rapides du terme de diffraction causé par le grand disque de rayon R₀ , il ne percevra qu’une moyenne locale :

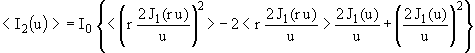
avec  , d’où et

On obtient ainsi :  

Le premier terme est grand mais à variation lente devant le terme suivant correspondant à l’intensité I₂ du petit disque :

Le contraste sera donc très faible mais on prévoit qu’en dehors de l’image géométrique, l’intensité pour la pupille complémentaire P₂ sera modulée par la diffraction du petit disque P₁ .

Remarque : on peut améliorer la visibilité de la figure de diffraction en remplaçant le disque unique de rayon R₁ par une multitude de petits disques identiques disposés aléatoirement sur la surface transparente du grand disque (poudre de lycopode) .

7.5. Simulations :                   

Ces figures de diffraction des pupilles P1 et P2 ont été obtenues pour r = 10 par simulation avec Maple V 4 :

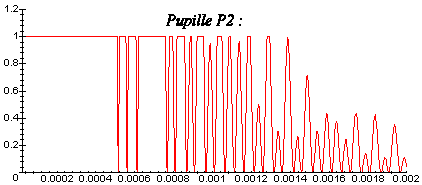Remarque : pour améliorer la visibilité des franges circulaires, on a volontairement surexposé de manière identique les deux  figures de diffraction.

On peut aussi visualiser les négatifs des images précédentes ...

.

retour: Conséquence