2. Constructions
du rayon réfracté :
2. Constructions
du rayon réfracté :
Charger
le fichier plage.fig 
que l’on ne sauvegardera
pas !
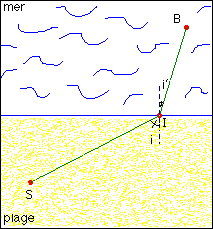
2.3.1. Problème du maître nageur :
Le maître nageur initialement au point S sur la plage doit
aller sauver un baigneur qui se noie dans la mer au point B .
Il court sur la plage à la vitesse v1 et il
nage à la vitesse v2 .
Il s'agit de déterminer le trajet optimum qui minimise le temps
de trajet.
Pour cela, on déplacera le point I à l’interface
entre la plage et la mer et on justifiera que les trajets sont rectilignes
sur la plage ou dans la mer.
On s’intéressera à la condition correspondante sur les
angles i et i’ .
On pourra comparer le résultat optimum avec le trajet direct correspondant
au segment SB .
2.3.2. Le Principe de Fermat :
On fera le lien avec une autre approche de l’optique géométrique, correspondant au principe de Fermat qui peut se formuler sous la forme suivante :
Le trajet suivi par la lumière, pour aller d’un
point à un autre, correspond un temps de parcours stationnaire (minimum,
maximum, …) .
retour: Huygens
Sommaire
Menu 
suite: lentille