ANNEXE A : Démonstration pour le cas simple

A.1. Notations :                  

On pose :
et

On admet les ordres de grandeur suivants:

Cela permettra de négliger systématiquement et   z²  mais pas de l’ordre de d² .

On conservera donc les termes du premier ordre en x , y et z , mais pas le second ordre.

Remarque:
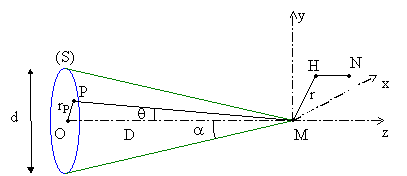
Vue la symétrie de révolution du problème, il est toujours possible de prendre le point N dans le plan Mxy par choix de l’axe Mx , soit  .

A.2. Distances :                  

·  

soit toujours en négligeant le second ordre ;

·   avec les mêmes hypothèses.

·   en utilisant l’expression de PN et en plaçant N en M avec  ;

·   directement .

A.3. Fonction de cohérence :                  

On cherche  .

On va déterminer  .

D’après l’évaluation des distances précédentes : .

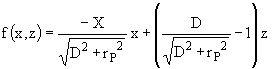On peut introduire les angles a et q tels que : (cf. figure)

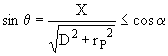et

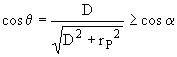
on obtient alors : dont on cherche un majorant.

Il faudra donc se limiter au domaine de x et z tel que  .

A.4. Largeur de cohérence :                  

On se limite ici au plan de front passant par M , soit  .

On a dans ce cas :

La condition sur x est donc :

Remarque 1 :  l’écart maximum est obtenu lorsque P est à la périphérie du disque, soit  .

Remarque 2 :  le plus souvent q est petit, ce qui permet d’imposer la condition :

Donc la largeur de cohérence est

A.5. Longueur de cohérence :                  

On se limite ici à l’axe Oz selon OM , soit  .

On a dans ce cas :

La condition sur z est donc :

Remarque 1 :  l’écart maximum est, ici encore, obtenu lorsque P est à la périphérie du disque,.

Remarque 2 :  si q est petit, cela permet d’imposer la condition :

Donc la longueur de cohérence est

.

retour: conclusion