ANNEXE B : Critère de cohérence pratique

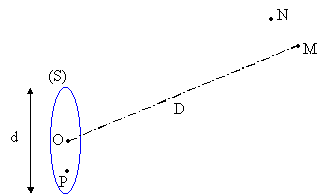
On cherche le lieu des points N tels que :   

 B.1. Principe :                  

La recherche systématique d’un maximum lorsque le point variable P se déplace sur la surface source n’est pas possible avec le logiciel Cabri Géomètre.

Aussi, on se contentera d’une évaluation approximative, pour N très voisin de M loin d’un disque source, déduite du cas où M est sur l’axe normal à la source passant par son centre.

La méthode utilisée part de l’hypothèse intuitive que le cas le plus défavorable à la cohérence est obtenu lorsque le point courant P se trouve à la " périphérie " du disque source.

B.2. Problème plan :                  

Dans le cas du voisinage de la normale, on se limite au problème à deux dimensions dans le plan de la figure contenant la normale et passant par M :

Remarque :  le point N est supposé dans ce plan …

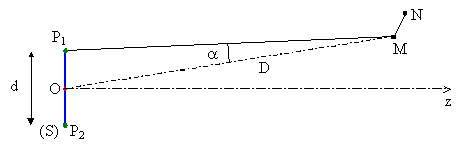
dans ce cas, en choisissant P en P₁ sur la périphérie et dans le plan de la figure, on a bien :

Remarque :
Dans le cas où N est extrêmement proche de M , choisir P en P₂ symétrique de P₁ par rapport à O , ne modifie pratiquement pas le résultat. On pourra s’en convaincre en utilisant les calculs classiques pour le dipôle électrostatique.

Cependant, pour les schémas pseudo-réalistes réalisés avec le logiciel Cabri Géomètre, cette condition n’est pas respectée et les résultats obtenus en P₁ et P₂ sont différents.

Pour prendre en compte cet écart, on évaluera les deux expressions et on choisira le maximum obtenu qui correspond au cas le plus défavorable :

   avec

B.3. Problème à trois dimensions :                  

Cependant, en dehors de ce voisinage de la normale, on ne peut se limiter à un problème plan. En effet, dans le cas particulier extrême où M est dans le plan de la source, il est évident que le choix de P₁ (ou P₂ ) ne convient plus :

on a alors :  !

(avec les approximations précédentes et pour P₁ ou P₂ )

Il faut alors considérer l’extension de la source orthogonale au plan de la figure et se placer dans le plan du disque :

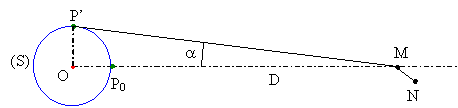
C’est maintenant le point P’ de la périphérie qui correspond à la situation la plus défavorable !

On a alors :

B.4. Choix final :                  

Dans le cas général, on se contentera de choisir le maximum des deux évaluations précédentes, soit ou  .

D’où la condition finale :

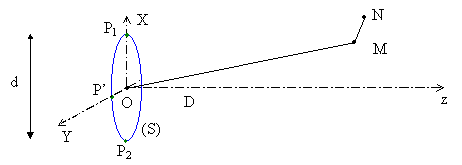
avec P₁ , P₂ et P’ sur la périphérie et tels que :

·  OP₁ et OP₂ dans le plan OXz contenant la normale Oz et le point étudié M ;

·  OP’ orthogonal à ce plan (selon OY ) ;

le point N restant très voisin de M .

B.5. Implémentation dans Cabri Géomètre :                  

Il s’agit de construire une procédure générale qui permettra d’affirmer si, oui ou non, le couple de points M et N voisins correspondent à des sources secondaires cohérentes spatialement pour une source large représentée par un disque de diamètre d .

Le logiciel Cabri permet l’évaluation facile de toutes distances et l’outil " calculette " donnera toutes relations simples entre ces distances. Cependant, il faut se souvenir que Cabri est conçu pour traiter le cas de la géométrie plane et il faudra s’adapter à ses limitations.

Il faudra donc introduire la direction orthogonale dans la même figure plane. Pour cela, on dessine un segment orthogonal à OM , de centre O et de longueur d , représentant la trace de la source dans le plan orthogonal à la figure initiale. On pourra alors placer P’ à une de ses extrémités.

Remarque :
En toute rigueur, il faudrait aussi modifier conjointement la position de N qui est placé (abusivement) dans le plan initial de la figure contenant la normale au centre du disque et le point M , mais les ordres de grandeurs relatifs permettent de s’affranchir de cette contrainte.
En effet, lorsque l’influence du point P’ devient prépondérante, c’est la longueur de la zone de cohérence qui limite la visibilité du phénomène et on se limitera donc au voisinage même de l’axe selon OM . De même, dans le cas contraire, au voisinage de l’axe normal, la symétrie de révolution n’est pas trop perturbée et l’orientation de MN autour de OM n’est pas cruciale.

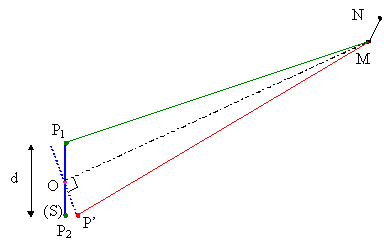
On pourra ainsi évaluer simultanément :

 , et

pour sélectionner leur maximum.

Il suffira alors de comparer ce maximum à pour discuter la cohérence spatiale mutuelle de M et N pour la source large (S) .

B.6. Conclusion :                  

Rappelons toutefois que l’évaluation du critère n’est qu’approximative et, qu’en dehors des situations particulières simples, les conclusions graphiques obtenues peuvent se révéler incorrectes, surtout si M et N ne sont pas très voisins. De plus, pour être lisible, les figures de Cabri Géomètre ne peuvent pas respecter des ordres de grandeur réalistes (schémas " pseudo-réalistes ") et les résultats obtenus dans les cas limites devront être discutés.

.

retour: Annexe A