3. Notion de zone de cohérence :

Traitons le cas d’une source (S) plane de dimension caractéristique d et d’origine O (ce sera son centre de symétrie s’il existe…) .

Soit P , le point courant sur cette surface.

On étudie le voisinage d’un point M suffisamment éloigné de la source (S) : . Pour cela, on introduit donc un point N tel que .

3.1. Définition :                  

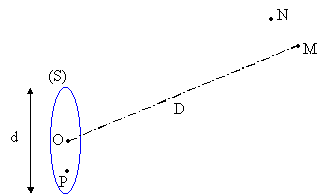
Le volume de cohérence autour du point M pour la source (S) , lieu des points N tels que :

où l est la longueur d’onde dans le milieu homogène considéré

(  est la fonction donnant le maximum des valeurs de son argument

lorsque le point courant P décrit le domaine (S) ) .

3.2. Justification :                  

Une source étendue (S) d'origine O , monochromatique éclaire deux sources secondaires ponctuelles M et N . Le point M servira de référence, N étant mobile au voisinage de M .

La cohérence spatiale des deux sources M et N sera assurée si l'écart des chemins optiques depuis P , point courant sur la source (S) , jusqu'aux points M et N dépend peu de la position de P sur (S) .

On compare donc les différences de marche entre N et M pour une source quelconque P et pour l'origine O . Si l'écart maximum est suffisamment faible devant la longueur d'onde l , l'état d'interférence résultant sera presque identique pour tous les points de la source large et tout se passera comme si la source était ponctuelle et il n'y aura pas brouillage de la figure d'interférence.

Remarque 1 :

Le choix d’une limitation à une demi longueur d’onde n’est pas significatif mais correspond à un bon ordre de grandeur.

Remarque 2 :

Il n’y a pas de limitation sur la position de M qui n’est donc pas restreint à être sur la normale à la source. On pourrait donc traiter le cas d’une source volumique.

.

retour: problème