4. Exemple simple :

On se limite ici au cas où M est sur la normale Oz à la source circulaire de diamètre d issue de son centre O .

On notera a le demi-angle d’ouverture du cône de sommet M sous lequel on voit la source (S) .

On introduit le point H la projection de N sur le plan de front passant par M et orthogonal à Oz . On appellera r la distance MH .

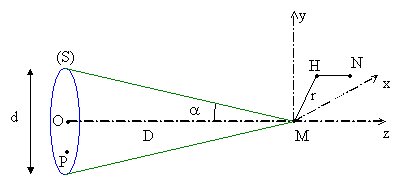
On se limitera à a petit conformément à et on a donc .

On recherche alors la zone de cohérence du point M relatif à la source (S) et on obtient :

4.1. La largeur de la zone de cohérence en M :                  

Il s’agit du diamètre de la section de la zone de cohérence avec le plan de front passant par M . Ceci correspond à la distance à l’axe maximum pour un point N dans ce plan de front ( N est très voisin de M ) ; soit :

                    (avec )

(cf. démonstration dans l'annexe A )

4.2. La longueur de la zone de cohérence en M :                  

Il s’agit de la longueur totale de la zone de cohérence selon l’axe, soit :

(cf. démonstration dans l'annexe A )

Attention :  cette longueur ne doit pas être confondue à la longueur de cohérence classique pouvant représenter la longueur d’un train d’onde.

Il s’agit alors de cohérence temporelle (onde non monochromatique) et non de cohérence spatiale.

4.3. La forme approximative de la zone de cohérence pour M :                  

Elle présente, bien sûr, une symétrie de révolution autour de l’axe Oz et elle dépend de la longueur d’onde et de l’éloignement relatif du point M considéré.

On pourra pour remarquer que, pour a petit, la longueur est très supérieure à la largeur et que pour des sources de lumière naturelle, la longueur des trains d’onde est, le plus souvent, plus faible que la longueur de la zone de cohérence. Mais ce n’est pas a priori le cas pour un LASER !

Remarque 1 :   pour le schéma pseudo réaliste ci-dessous, pour représenter une largeur non négligeable en même temps que la position relative de la source (S) , la distance n’est pas très supérieure à d et le point N n’est plus voisin de M pour toute la zone de cohérence ; dans ce cas, l’évaluation précédente de la longueur n’est donc plus valable.

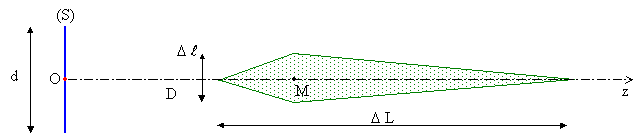
 Simulation  avec Cabri Géomètre

 Remarque 2 :   si on se contente d’étudier les points N dans le plan de front de M , la seule notion importante est la largeur de cohérence.

 Remarque 3 :  en dehors de la direction normale à la source, on constate des modifications significatives que pour des directions très obliques. Sinon les résultats restent très comparables.

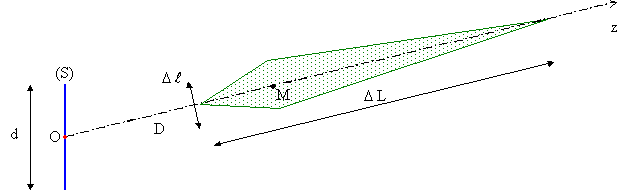
   Simulation  avec Cabri Géomètre

Remarque 4 :  les schémas précédents sont obtenus avec le logiciel de géométrie dynamique Cabri Géomètre en utilisant une méthode pratique approchée pour l'évaluation du critère de cohérence spatiale qui est décrite dans l'annexe B .

4.4. Conclusion :   représentation simplifiée au voisinage de la normale à la source                  

Pour des points N voisins du plan de front de M , on pourra se contenter d’une représentation simplifiée ne mettant en évidence que la largeur de cohérence dans une direction donnée (peu inclinée par rapport à la normale) quelle que soit la distance D du point M à la source.

On introduit ainsi un cône de sommet O , d’axe dirigé vers M , et de demi-angle d’ouverture :

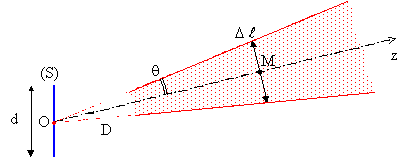
Remarque 1 :   comparaison de la zone de cohérence spatiale effective et du modèle simplifié n’exploitant que la largeur de cohérence réalisée par simulation avec Cabri Géomètre :

   Simulation  avec Cabri Géomètre

 Remarque 2 :   il est intéressant de remarquer que le demi-angle d’ouverture de la zone de cohérence spatiale est du même ordre que celui obtenu pour le phénomène de diffraction pour l’ouverture correspondant à la source.

.

retour: définition