7. Application au coin d’air :

Il s’agit ici de retrouver (et préciser) les résultats classiques trop souvent admis sans justification et, surtout, sans discussion.

7.1. Cas étudié :                  

On considère une source monochromatique " large " (disque) éclairant un coin d’air de faces planes (M₁) et (M₂) formant un dièdre de très faible angle e  . Soit O son " centre " suffisamment éloigné du coin d’air et au voisinage des normales aux faces sur l’arête du dièdre pour pouvoir considérer que les rayons incidents utiles arrivent sur le coin d’air d’épaisseur très petite en incidence faiblement oblique.

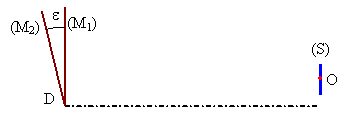
D’autre part, on se limitera à traiter les rayons lumineux contenus dans le plan de la figure passant par le centre O et perpendiculaire à l’arête du dièdre. La justification de cette limitation peut être déduite de l’invariance du problème par translation selon l’arête et que les termes correctifs correspondants sont d’ordre supérieur (au moins d’ordre 2 ) .

De même, pour simplifier le problème, on ne prendra en compte aucune réfraction pendant la traversée des faces du coin d’air. Cette hypothèse sera d’ailleurs rigoureusement vérifiée pour le coin d’air équivalent obtenu pour l’interféromètre de Michelson réglé au contact optique, mais avec des miroirs non strictement perpendiculaires.

7.2. Localisation pour la division d’amplitude stricte :                  

Pour un rayon issu du centre O subissant une division d’amplitude par réflexion-transmission en I sur (M₁) et une simple réflexion sur (M₂) , les deux rayons émergeants se coupent au point A₀ . Il est commode, pour tracer les rayons correspondants et obtenir leur intersection A₀ , d’introduire les images O₁ et O₂ de O par les miroirs (M₁) et (M₂) .

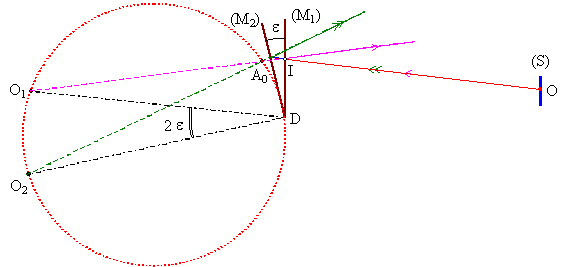
On montre, par des arguments de géométrie élémentaire, que tous les points d’intersection A₀ obtenus par déplacement du point I sur (M₁) , ont pour lieu un cercle passant par l’arête du dièdre et par les images O₁ et O₂ .

   Simulation  avec Cabri Géomètre   ou   figures animées

Remarque 1 :  rappelons que nous ne traitons ici que la source " ponctuelle " O et que le cercle obtenu serait légèrement différent pour un autre point P de la source (S) .

Remarque 2 :  dans le cas où on éloigne la source (S) à l’infini, les images O₁ et O₂ sont aussi rejetées à l’infini et le cercle tend vers une droite passant par D et orthogonale à la bissectrice de l’angle de sommet D et dont les côtés sont dirigés vers O₁ et O₂ ; on retrouve alors le résultat classique correspondant à une localisation sur un plan passant par l’arête du dièdre et faisant un angle très faible par rapport aux faces du coin d’air. Mais répétons encore que cette localisation précise change lorsque l’angle d’incidence est modifié, ce qui est forcément le cas pour une vraie source " large " qui justifie le choix de la division d’amplitude !

   Simulation  avec Cabri Géomètre

Remarque 3 :  on peut aussi montrer que le point A₀ appartient à un autre cercle passant par l’arête D , par le point d’incidence I sur (M₁) et centré sur l’autre face (M₂) .

7.3. Utilisation des zones de cohérence :                  

Pour déterminer le domaine de visibilité des franges, c’est à dire le lieu des points A tels que le contraste n’est pas négligeable, on peut exploiter les propriétés des zones de cohérence.

Cependant, il va se poser deux difficultés de natures totalement différentes :

·  la division d’amplitude est supposée approximativement respectée, et la notion de largeur de cohérence n’est plus suffisante pour discuter de la visibilité des interférences en A ; il faut donc considérer aussi la longueur de la zone de cohérence et ne pas se limiter à la représentation simplifiée qui a permis de choisir la division d’amplitude.

·  le moyen d’observation utilisé pour visualiser les interférences joue souvent un rôle fondamental dans la figure observée ; en effet, le diamètre d’ouverture de l’œil ou de la lentille de projection limite l’extension de la source utile. C’est pour cela que des interférences peuvent être bien visibles à l’œil, mais n’apparaissent pas par projection à l’aide d’une lentille de grande ouverture. On supposera ici que l’ouverture du dispositif d’observation est suffisamment grande pour ne pas modifier les dimensions de la source primaire utile.

7.4. Simulation avec Cabri Géomètre :                  

Il n’existe pas de méthodes simples pour évaluer l’extension effective de la zone de localisation des interférences ; aussi, on se contentera d’une simulation effectuée avec le logiciel de géométrie (plane) dynamique Cabri Géomètre.

Rappel :
les schémas sont obtenus en utilisant une méthode pratique approchée pour l'évaluation du critère de cohérence spatiale qui est décrite dans l'annexe B .

Le schéma suivant met en évidence le lieu des points A permettant l’observation d’interférences pour le coin d’air de faces (M₁) et (M₂) avec la source (S) monochromatique de longueur d’onde l (disque de centre O ) :

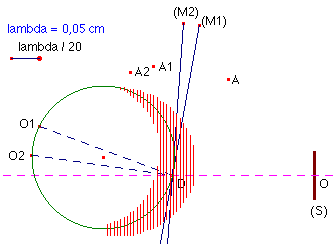
On obtient (dans le plan de la figure) une zone de visibilité des interférences localisée au voisinage du cercle précédent correspondant au point A₀ (localisation d’amplitude stricte) .

Mais l’ensemble du cercle n’est pas valide : le domaine trop proche des images O1 et O2 de O ne permet pas un contraste suffisant.

D’autre part, au voisinage de l’arête D du dièdre, il y a un fort élargissement de la zone de visibilité.

Globalement on obtient un " croissant " dont la partie épaisse recouvre le coin d’air au voisinage de son arête :

Le domaine de visibilité est donc surtout localisé " sur " le coin d’air

(comme l’affirme le résultat classique du cours; cependant ce résultat ne présente pas le caractère rigoureux que certains documents affirment)

   Simulation  avec Cabri Géomètre

Remarque :

Pour rendre le schéma plus lisible, il est nécessaire de ne pas respecter des échelles réalistes :

·  la longueur d’onde choisie ne respecte pas du tout les ordres de grandeur de la lumière visible et l’on constate une forte diminution du domaine de visibilité pour des longueurs d’onde décroissantes ; la localisation des interférences est donc plus " proche " du coin d’air.

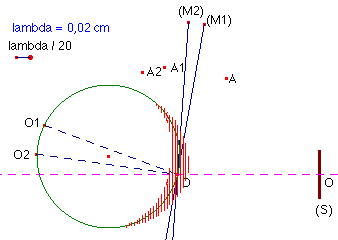
·  l’angle du coin d’air est généralement beaucoup plus faible que celui représenté sur les schémas précédents, ce qui se traduit par l’effet inverse, soit un élargissement du domaine d’interférences.

.    Simulation  avec Cabri Géomètre

retour: division d'amplitude