2.1.1. La Méthode des Moindres Carrés classique

(ou Méthode du Modèle selon Monsieur Trigeassou, décrite et exploitée dans le Compte Rendu des Journées Informatique et Sciences Physiques de GRENOBLE de 1988 et dans son livre 'Recherche de Modèles Expérimentaux' ) .

2.1.1.1. Critère Quadratique

2.1.1.2. Hypothèses de validité

début

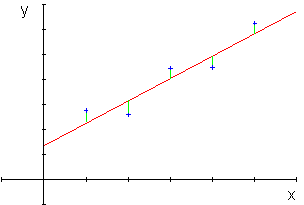
Cette méthode s'applique à n'importe quelle fonction, et consiste donc à déterminer les r paramètresen minimisant le Critère Quadratique  J  correspondant à la somme des carrés des écarts entre la variable expliquée et la valeur correspondante de la fonction modèle optimisée:
                                     

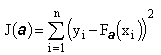
On constate que cette méthode escamote, apparemment, la dispersion résultant des incertitudes des mesures expérimentales.

début

En toute rigueur, cette méthode n'est applicable que pour une fonction linéaire par rapport aux paramètres:
                                                 

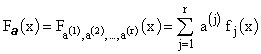
Mais on pourra admettre l'extension de son application au cas non linéaire pour un ajustement suffisamment "serré", c'est à dire en supposant des écarts suffisamment faibles entre points expérimentaux et courbe théorique pour pouvoir réaliser une linéarisation locale aux voisinages de ces points.

Remarque 0: cette condition est toujours réalisée pour les lois proposées en Travaux Pratiques de Sciences Physiques, ce qui n'est pas le cas pour d'autres disciplines comme les Sciences de la Vie et de la Terre ou en Economie.

De plus, il faut rappeler les hypothèses qui justifient théoriquement sa validité:

• les variables explicatives sont supposées connues avec une précision parfaite;
•  les variables expliquées doivent être affectées d'incertitudes indépendantes, de valeur moyenne nulle et de même écart-type pour tous les  .

De telles conditions sont, le plus souvent, irréalistes, mais en admettant leur validité, elles permettent, d'une part, de ne pas avoir à évaluer quantitativement la précision des mesures, et d'autre part, de conduire à des expressions simples et à des résultats souvent satisfaisants.

Cependant, a contrario, elles ne permettent pas d'évaluer correctement la précision sur les paramètres obtenus et, plus grave, elles risquent d'introduire, dans certains cas, un biais dans l'évaluation de ces paramètres.

Remarque 1: la distribution des incertitudes est en général gaussienne, mais la nature effective de la distribution statistique intervient peu dans les conclusions. On dit alors que l'on a une méthode robuste.

Remarque 2: la distribution des n couples de mesures utilisés n'est pas sans conséquence sur les résultats obtenus. Il vaut mieux une distribution 'harmonieuse' sur l'ensemble du domaine étudier et, surtout, ne pas négliger les zones où se produisent des phénomènes particuliers (extremums, points d'inflexions, etc. ) .

retour: Méthodes