(décrite par Monsieur Ruhla dans le B.U.P. n° 702 et dans son livre 'La Physique du Hasard ' )
2.1.2.1. La Régression Linéaire (ou Modèle Linéaire)
Les logiciels informatiques (et les calculettes) proposent systématiquement ce qu'il est convenu d'appeler la Régression Linéaire, c'est à dire d'appliquer la Méthode des Moindres Carrées au cas particulier de la fonction affine:
![]()
Dans ce cas, les estimateurs ![]() et
et ![]() des paramètres
a et b se calculent simplement en exprimant les conditions:
des paramètres
a et b se calculent simplement en exprimant les conditions:
![]() et
et ![]()
ce qui conduit à:
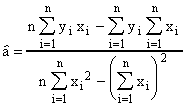 et
et
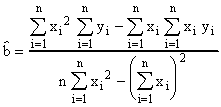 .
.
On peut exprimer plus simplement l'équation de la droite de
régression en utilisant les caractéristiques statistiques
estimées de la distribution des points de mesures:
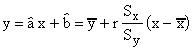
où l'on a introduit les moyennes
![]() et
et
![]() et les
écart-types
et les
écart-types
![]() et
et
![]() des distributions
des distributions
![]() et
et
![]() ainsi que le
coefficient de corrélation
linéaire r entre ces deux distributions (cf.
Annexe) .
ainsi que le
coefficient de corrélation
linéaire r entre ces deux distributions (cf.
Annexe) .
On constate alors que la droite de régression passe par le barycentre des points de mesure.
Pour des fonctions non linéaires, on peut parfois se ramener au cas affine précédent par des changements de variables. On parle alors d'Anamorphose (ou changement de forme) .
On utilisera les notations suivantes: ![]()
puis on appliquera la Méthode de Moindres
Carrés pour estimer les coefficients c et
d ,
et on en déduira
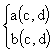 .
.
Exemple classique:
![]() transformé
par transformation logarithmique en
transformé
par transformation logarithmique en ![]() où:
où:
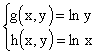 et
et
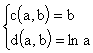 soit
soit
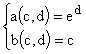
Les calculettes et la plus part des logiciels standards proposent des régressions 'non' linéaires de ce type (régression de puissance, exponentielle, logarithmique, etc. ) . En fait, le traitement effectif utilise l'Anamorphose correspondante.
Les hypothèses à respecter pour un traitement valide restent
les mêmes que pour le traitement général, mais doivent
être appliquées aux nouvelles variables, ce qui est encore
plus discutable que par la méthode directe.