3.3.1. Domaine étudié
3.3.1. Domaine étudié
La suite du traitement ne sera valide que pour une estimation suffisamment 'bonne' des paramètres optimisés.
En effet, les valeurs obtenues des paramètres seront utilisées pour déterminer leurs précisions et des écarts significatifs conduiraient à un biais dans l'estimation correspondante.
Dans tous les cas, il faudra disposer des informations sur les distributions statistiques des mesures effectuées, à savoir de leur écart-type dans le cas d'une distribution gaussienne.
Si cela ne pose pas de difficulté dans le cas de la Méthode des Ellipses car la connaissance des écart-types est un présupposé de la méthode, au contraire, cela pose problème dans la Méthode des Moindres Carrés:
Le Critère Quadratique J ne fait pas intervenir directement les incertitudes de mesure !
En fait, lorsque les hypothèses de validité sont respectées
(grandeurs explicatives infiniment précises et grandeur expliquée
y d'écart-type uniforme 
) ,
le Critère Quadratique minimum conduit à un estimateur
satisfaisant de :
.
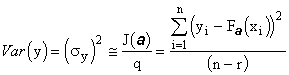On doit remarquer que la valeur estimée de dépend
de la valeur des paramètres obtenus par l'optimisation et que le nombre
de mesures n est, le plus souvent, très réduit. Ces phénomènes
conduisent à une estimation de médiocre précision et relativement
peu fiable.
Titre, résumé
retour: Précision
Sommaire
suite:
Nature