2.2.2. La Méthode
des ELLIPSES ou du Chi-Deux sur deux variables 2.2.2. La Méthode
des ELLIPSES ou du Chi-Deux sur deux variables
(décrite par Yves Cortial dans les articles discutant la Méthode des Moindres Carrés paru dans le B.U.P. n° 725 ou dans Compte Rendu des Journées Informatique et Sciences Physiques de TOULOUSE de 1990 ) .
2.2.2.1. Hypothèses de validité
2.2.2.2. Nouvelle expression
du
2.2.2.5. Interprétation géométrique
2.2.2.6. Comparaison aux rectangles d'incertitude
2.2.2.1.
Hypothèses de validité
début
On ne néglige plus, ici, les incertitudes sur les variables explicatives
, et on attribue
à chacune l'écart-type
,
en plus de l'écart-type
de
chaque variable expliquée 
.
Toutes les autres hypothèses décrites dans le paragraphe précédent sont supposées respectées; en particulier, on admet toujours l'indépendance des incertitudes et l'absence d'erreurs systématiques.
2.2.2.2. Nouvelle expression
du
début
Dans le cas d'incertitudes non exagérées (ajustement 'serré') ,
on en déduit un 
généralisé,
sous la forme:
début
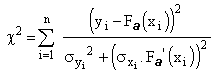
Le dénominateur de chaque terme étend la notion d'écart-type pour un problème à variables multiples dans les hypothèses choisies.
En effet,
correspond
à une distribution statistique gaussienne centrée (valeur moyenne
nulle) et de variance
(d'après la 'propagation des erreurs' dans le cas des écarts faibles) .
Les grandeurs 
correspondent
donc à des distributions gaussiennes centrées
réduites (d'écart-type unitaire) .
Or le à
q degrés de liberté peut être considéré comme
la somme des carrés de q variables gaussiennes centrées réduites
indépendantes (cf. Annexe) .
Ici, avec r paramètres à déterminer et
n points de mesure, le nombre de degrés de liberté est
bien
.
Remarque:
L'expression précédente peut se généraliser au cas
des n valeurs des m variables explicatives 
sous la forme:
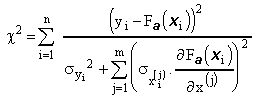
2.2.2.4. Critère proposé
début
Afin de rendre l'ordre de grandeur du critère indépendant du nombre de mesures (normalisation) , il est commode de choisir comme CRITERE de l'optimisation:
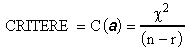
oùest
le nombre de degrés de liberté du système.
Pour un tel choix, le CRITERE doit avoir une valeur proche de
l'unité pour une modélisation satisfaisante (d'après
les propriétés de la distribution du
et
la discussion de la
validité ) .
On pourra donc vérifier immédiatement la validité de cette modélisation.
Cependant, la valeur du CRITERE obtenu dépend de l'estimation des écart-types des mesures, et une valeur improbable peut provenir d'une mauvaise évaluation de ces écart-types (cf. suite) .
début
La question qui se pose maintenant est celle-ci:
A-t-on obtenu ainsi la "meilleure" évaluation possible des paramètres ?
D'un point de vue statistique, un estimateur doit être convergent, sans biais, efficace et, si possible, robuste (cf. en annexe pour la définition de ces propriétés) .
Il s'agit de justifier ici que les méthodes proposées respectent effectivement ces conditions dans leur domaine de validité.
La justification correspondante est basée sur la Théorie du Maximum de Vraisemblance qui consiste à supposer que l'événement qui se produit est le plus probable, c'est à dire celui qui correspond au maximum de la densité de probabilité.
Dans le cas linéaire, on peut montrer qu'elle conduit à des estimateurs des paramètres sans biais de variance minimale (théorème de Gauss-Markov) .
L'ajustement obtenu sera donc efficace et correspondra à la 'meilleure' évaluation possible des paramètres.
> Application à un point de mesure:
La densité de probabilité pour le point effectif 
correspondant au point expérimental
peut
s'écrire:
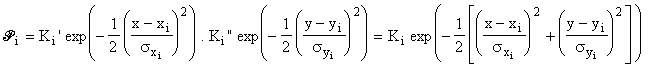
en supposant les distributions en x et y
gaussiennes et indépendantes.
On constate que les courbes d'isodensité correspondent à des
ellipses de dispersion centrées
sur le point, homothétiques
et d'équation:
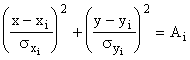
On représente généralement l'ellipse
de dispersion unitaire correspondant à 
et dont les demi-axes sont égaux aux écart-types des variables
correspondantes.
On appellera 
le point
le plus probable de la courbe 
,
c'est à dire celui qui correspond à la densité maximum.
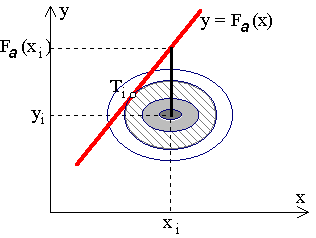Il correspond donc au point
de tangence de la courbe avec une des ellipses précédentes
d'équation:
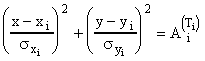
où 
est
déterminé par la condition de tangence.
En effectuant un développement au premier ordre, on obtient:
!
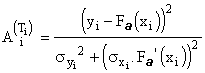> Application à l'ensemble des points de mesure:
Les mesures étant indépendantes, la densité de
probabilité correspondant à l'ensemble des points les plus
probables peut donc s'écrire:
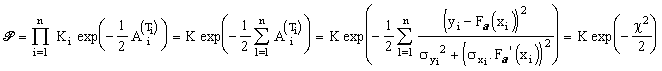
Une densité maximum correspond effectivement à un minimum du
.
2.2.2.6. Comparaison aux rectangles
d'incertitude
début
Il est intéressant de revenir sur la méthode traditionnelle d'ajustement qui consiste à faire passer graphiquement une droite le mieux possible dans les rectangles centrés sur les points expérimentaux et de demi-cotés égaux aux incertitudes absolues correspondantes.
La Méthode des Ellipses correspond exactement à cette technique à condition de considérer le phénomène des incertitudes comme probabiliste et dont on connaît les écart-types:
De plus, l'introduction du CRITERE des Ellipses rend la méthode quantitative et permet une résolution numérique pour des fonctions quelconques, mais il est tout à fait satisfaisant de valider théoriquement une méthode 'historique' dont la justification peut se trouver dans le simple bon sens physique.
Titre, résumé
retour: Méthodes
Sommaire
suite:
Validité