3.2. Discussion de la validité d'un modèle proposé

La vérification de la loi proposée devra être validée quantitativement, essentiellement par l'évaluation d'une probabilité de fiabilité (intervalle de confiance) .

Il reviendra alors à l'expérimentateur le rôle de fixer les valeurs limites tolérables de cette probabilité en fonction des hypothèses de travail réalisées.

Seules les méthodes basées sur la distribution du proposent, par nature, une telle probabilité. En effet, le Critère Quadratique de la Méthode des Moindres Carrés ne possède pas de référence absolue permettant d'interpréter directement la valeur de ce critère.

3.2.1. Les dangers du coefficient de corrélation linéaire

3.2.2. La médiane de la distribution du CHI-DEUX

3.2.3. Exemple 1

3.2.4. Interprétation de la valeur du CRITERE

début

Cependant, lors d'une Régression Linéaire, après une Anamorphose éventuelle, la Méthode des Moindres Carrés fait apparaître un indicateur de l'ajustement:

le coefficient de corrélation linéaire    (cf. Annexe) .

Les outils informatiques fournissent toujours la valeur de r en sus des estimateurs des paramètres de l'ajustement, et on affirme que:
          l'alignement des points sera correctement réalisé si sa valeur absolue est proche de l'unité

(en fait, r prend toute valeur comprise entre -1 et +1 suivant que la pente de la droite de régression est négative ou positive et que les points considérés sont plus ou moins éloignés de cette droite) .

En fait, ce critère d'ajustement n'est pas fiable surtout si l'on s'intéresse à la vérification d'une modélisation précise (cf. Remarque 0 de la présentation de la Méthode des Moindres Carrés) .

En effet, on peut obtenir une valeur très proche de l'unité pour des modèles incorrects (  par exemple) et, par contre,  une valeur quasi nulle pour des points parfaitement alignés.

L'exemple classique correspondant est celui de l'étude du produit pour l'isotherme d'un gaz réel sous des pressions faibles. Dans ce cas, le gaz réel est proche du gaz parfait, et le produit est pratiquement constant.
Les points sont bien alignés, mais il n'y a pas corrélation entre les variables et on doit trouver r strictement nul pour .

Il ne faudra pas oublier non plus qu'il s'agit du coefficient de corrélation linéaire et que les imperfections peuvent provenir aussi bien d'une distribution aléatoire des points de mesure que d'une distribution ordonnée non linéaire non prise en compte dans la modélisation proposée.

On se référera à la figure ci-dessous où les quatre 'nuages' de points ont mêmes moyennes, mêmes variances et même coefficient de corrélation.

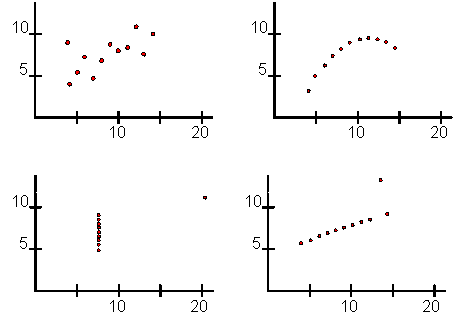
L'interprétation de r n'est significative que pour le premier nuage et l'on constate que sa valeur est très influencée par les points extrêmes ou aberrants:
         les conclusions déduites ne seront donc pas robustes.

début

Une vérification plus satisfaisante est basée sur la densité de probabilité associée à la distribution du à q degrés de liberté (cf. Annexe) .

Cette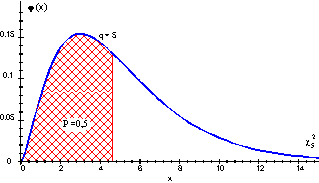 distribution n'est pas symétrique et, bien que l'espérance mathématique soit égale à q , la médiane est légèrement inférieure à q .

Rappelons que la médiane de la distribution est caractérisée par sa probabilité donnée par sa fonction de répartition:

Remarque: On a, bien sûr,

En considérant que la médiane est voisine de q , cela justifie le choix de la définition du CRITERE des Ellipses:
              .

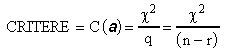La valeur du CRITERE sera donc directement liée à la probabilité associée et cette valeur devrait bien être voisine de l'unité pour une estimation optimale.

Cette fonction de répartition est tabulée (cf. ouvrages spécialisés) ou calculable numériquement et on pourra donc en déduire la probabilité d'obtenir un CRITERE supérieur (ou inférieur) à la valeur calculée et de préciser certaines limites intéressantes selon le nombre de degrés de liberté.

On trouvera dans l'exemple 1 ci-dessous, quelques valeurs particulières.

début

Probabilités théoriques pour que le CRITERE dépasse une certaine valeur:
 

pour

 

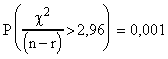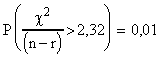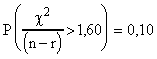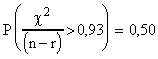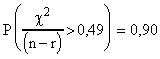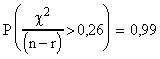pour

début

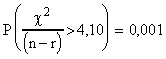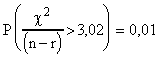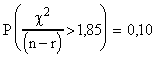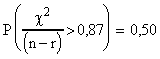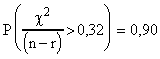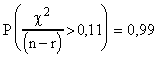La fonction de répartition précédente permettra donc une évaluation quantitative de la probabilité de l'écart par rapport à cette valeur optimale.

Il sera, en particulier, intéressant de préciser le Domaine de Confiance à un seuil déterminé (  par exemple) et correspondant donc à une probabilité donnée et caractérisé par les limites et telles que:

Les limites et dépendront du nombre de degrés de liberté .

Par exemple pour  , on obtient une Médiane à 0,870 et des Domaines de Confiance suivant le seui l:
 

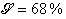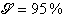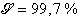Ainsi, toute valeur obtenue du CRITERE qui s'écarte sensiblement de l'unité doit être tenue pour suspecte.

On peut se reporter à l'exemple 1 ci-dessus afin de constater que les probabilités théoriques décroissent très vite en s'éloignant de la valeur optimale.

En particulier, il faut remarquer qu'un CRITERE trop petit est aussi improbable qu'un CRITERE trop grand !

Cependant, aucune conclusion systématique ne peut en être déduite, car l'évaluation du CRITERE dépend trop des hypothèses réalisées, en particulier sur l'estimation des écart-types.

Ainsi un CRITERE trop grand peut provenir d'une mauvaise modélisation ou d'une évaluation optimiste des écart-types (trop petits) .

De même, un CRITERE trop petit provient sans doute d'une évaluation pessimiste (écart-types trop grands) . Une telle situation n'assure pas la validation du modèle !

Par exemple, une majoration systématique d'un facteur trois, dans l'évaluation de ces écart-types, se traduit par un critère pratiquement dix fois trop faible !

Ainsi, une évaluation trop pessimiste peut masquer un mauvais ajustement de la loi proposée !

Cependant, dans ce cas, on pourra toujours comparer efficacement deux modélisations concurrentes du même phénomène physique.

En fait la valeur de ce CRITERE a pour rôle de servir d' avertisseur beaucoup plus performant et sélectif que le Facteur de Corrélation traditionnel de la Méthode des Moindres Carrés (bien qu'il ne faille pas oublier la difficulté de sa détermination absolue) .

retour: Validité