3.3.3. Nature des distributions statistiques des paramètres

Une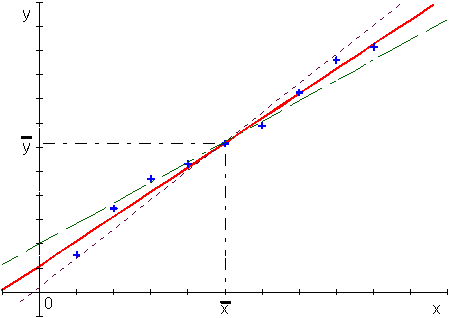 difficulté supplémentaire apparaît lorsque l'on étudie les distributions statistiques des paramètres:
      a priori, elles sont corrélées.

On peut mettre en évidence graphiquement ce phénomène en se limitant au cas de la Régression Linéaire sous la forme  .

En effet, lorsque l'on trace les droites de pentes "extrémales", on se rend compte qu'elles passent par le point 'moyen' du nuage de points expérimentaux. Dans ce cas, la valeur du paramètre b , correspondant à l'intersection de la droite considérée avec l'axe des ordonnées, est directement liée à la pente a .

Cette corrélation disparaît lorsque le point "moyen" se trouve sur l'axe des y , soit avec et on a alors  .

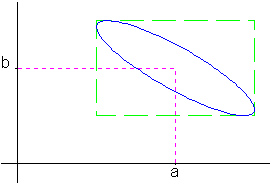
On pourra vérifier l'importance de cet effet en étudiant les courbes d'isodensité en a et b correspondantes dessinées ci-dessous (ellipses de dispersion unitaires par exemple, si les distributions sont gaussiennes) :
 

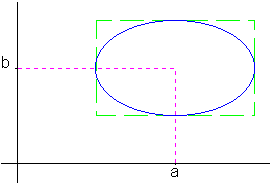
Avec corrélation	Sans corrélation

Ainsi, en toute rigueur, il faudrait donc introduire la covariance correspondante (ou le coefficient de corrélation) , mais on se contentera, le plus souvent, d'évaluer l'écart-type de chaque paramètre.

Remarque: Sur le deuxième graphe, on constate que la non corrélation des distributions ne signifie pas l'indépendance des estimations:
        dans ce cas, les écarts maximums en b seront obtenus uniquement pour a optimal.

retour: Précision