3.3.4. Evaluation par le calcul

La relation théorique entre les paramètres statistiques des paramètres obtenus par optimisation et les écart-types des points de mesure est présentée dans la documentation JEULIN du logiciel ACTILAB écrit par Messieurs Bougenière, Duboc et Petrisot. On trouvera d'autres informations, concernant le cas linéaire, dans l'article de Monsieur Journeaux paru dans le B.U.P. n° 752 (cf. Bibliographie) .

L'ordinateur est parfaitement adapté au calcul correspondant, mais si les résultats numériques obtenus sont intéressants, la méthode et sa démonstration sort du cadre de cette présentation.

Toute fois, il faut se souvenir que la validité des conclusions obtenues est directement liée à une estimation correcte des incertitudes des mesures expérimentales.

---

3.3.5. Utilisation des courbes isocritères            

Monsieur Trigeassou décrit leur utilisation pour la Méthode des Moindres carrés, mais leur tracé prend tout son intérêt en utilisant la 'métrique' dugénéralisé.

Dans le cas à deux paramètres a et b , la fonction définissant le CRITERE de la Méthode des Ellipses est une fonction de deux variables présentant un minimum pour les valeurs de a et b choisies. On notera la fonction et le minimum correspondant.

Une telle fonction peut être représentée par une surface dans l'espace à trois dimensions caractérisées par les axes orthogonaux sur lesquels seront reportés les valeurs de a , b et .

Au voisinage du minimum, on supposera que l'approximation linéaire s'applique, ce qui permettra d'assimiler la surface correspondante à un paraboloïde d'axe de symétrie vertical (cf. exemple 2 ) .
 

Exemple 2 :
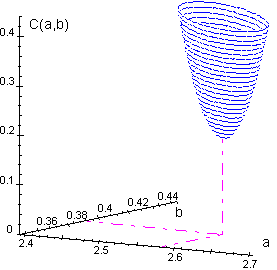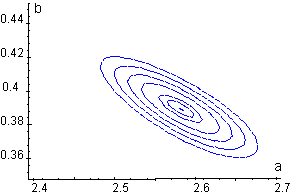Surface C(a,b)	Courbes isocritères

On s'intéresse ici à l'intersection de ce paraboloïde avec un plan horizontal, soit la courbe isocritère d'équation  .

On peut montrer alors qu'il y a équivalence entre ces courbes isocritères et les courbes d'isodensité pour les distributions gaussiennes.

En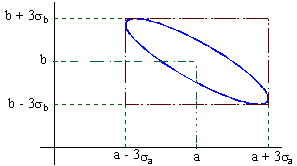 particulier, la courbe d'isodensité d'extension égale à  fois l'écart-type, est caractérisé par la valeur du CRITERE :

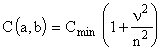
où n est le nombre de points expérimentaux.

On obtient ainsi une ellipse inscrite dans un rectangle de demi-cotés et  .

On choisit, le plus souvent, ( Règle des 3 sigmas ) .

retour: Précision