4.2.1. Résultats
obtenus
![]() début
début
![]()
La minimisation du Critère Quadratique,
pour la fonction non linéaire ![]() ,
ne pose aucune difficulté numérique et l'on obtient:
,
ne pose aucune difficulté numérique et l'on obtient:
![]() et
et
![]()
avec ![]() et
et
![]()
Le tracé correspondant est donné par la figure
1 où les points expérimentaux sont représentés
par leurs "Ellipses de Dispersion Unitaires"
de demi-axes ![]() et
et ![]() (on a superposé,
en pointillés, la courbe obtenue par la Méthode
des Ellipses sur la figure) .
(on a superposé,
en pointillés, la courbe obtenue par la Méthode
des Ellipses sur la figure) .
Figure 1: Méthode du
Modèle ( Moindres Carrés )
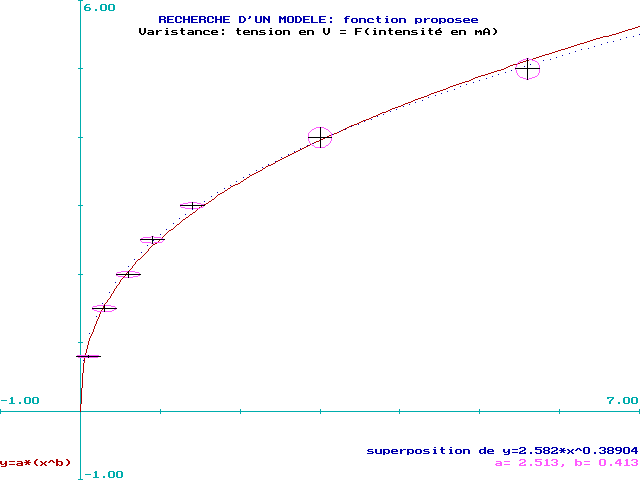
On constate un léger désaccord entre les deux courbes qui peut se justifier en considérant les faibles valeurs de x (cf. figure 2 ) .
Figure 2: Méthode du
Modèle ( Moindres Carrés ) au voisinage de l'origine

En effet, la Méthode des Moindres Carrés
minimise les termes en ![]() ,
donc selon un segment vertical. Alors que la Méthode
des Ellipses, comme son nom l'indique, minimise l'ellipse tangente à
la courbe, cette ellipse restant homothétique à l'Ellipse
de Dispersion Unitaire (cf. figure 3 ) .
,
donc selon un segment vertical. Alors que la Méthode
des Ellipses, comme son nom l'indique, minimise l'ellipse tangente à
la courbe, cette ellipse restant homothétique à l'Ellipse
de Dispersion Unitaire (cf. figure 3 ) .
Figure 3: Ellipse tangente à la courbe
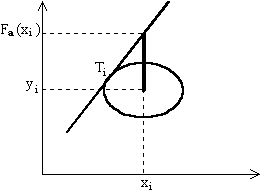
Remarque: Le point de tangence![]() est
"le point le plus probable" de la courbe correspondant au point expérimental
est
"le point le plus probable" de la courbe correspondant au point expérimental
![]() .
.
Même avec des précisions comparables, pour une fonction ayant
de très fortes variations de pente , les résultats sont
profondément modifiés (cf. figure
4 ) .
Figure 4: Influence de la pente de la courbe |
||
|
|
|
1écart-type en y , |
||
3/4 écart-type |
1/2 écart-type |
1/8 écart-type |
pour l'ellipse. |
||
De plus, dans le cas de la V.D.R. étudiée, avec les échelles représentatives, les Ellipses de Dispersion Unitaire sont fortement "allongées" selon les x , ce qui aggrave les différences entre les deux méthodes d'optimisation.
Ainsi, la courbe obtenue par la Méthode des Moindres Carrés passe plus près des points expérimentaux aux faibles valeurs de x , alors que celle déduite de la Méthode des Ellipses permet un décalage horizontal.