4.3. Moindres Carrés après
Anamorphose 4.3. Moindres Carrés après
Anamorphose
début
On obtient une fonction linéaire en prenant le logarithme népérien (ou décimal) de la relation précédente.
Soit: 
(ou 
)
C'est la méthode proposée par la documentation JEULIN
"en représentant 
sur du papier log-log".
C'est, aussi, la même méthode qui est suivie par les calculatrices
plus sophistiquées qui proposent divers modèles de régression
dont la fonction Puissance: 
(cf. la TI-81 par exemple ) .
Cela revient à réaliser l'anamorphose
correspondante avant d'effectuer la Régression
Linéaire classique sous la forme 
avec:
 |
 |
(  ) |
 |
 |
début
On obtient alors les résultats numériques suivants:
 |
 |
 |
 |
 |
 |
On constate que le Facteur de Corrélation r est très proche de UN , bien que l'alignement des points ne soit pas parfait, comme le montre la figure 5 .
Figure 5: Moindres Carrés
après Anamorphose
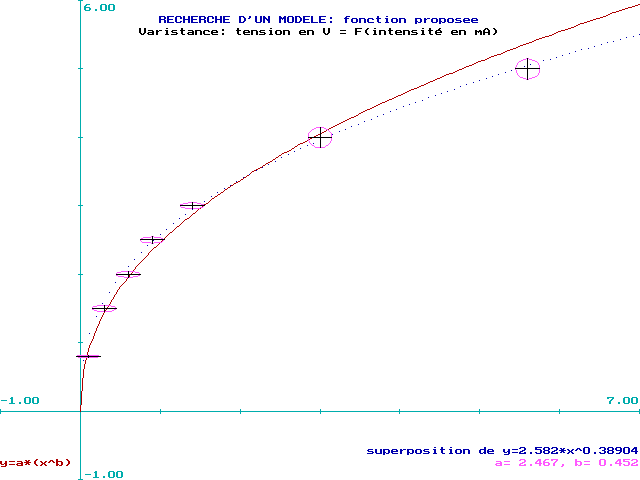
De plus, le tracé de la fonction initiale montre une augmentation de la discordance pour les fortes valeurs de x (cf. figure 6 ) .
Cela est dû à l'accentuation du défaut précédent par le changement de variables réalisé.
En effet, d'après l'approximation différentielle 
,
on prévoit l'aggravation de la contrainte pour les faibles valeurs de
y (et donc de x ) .
Le facteur 5 , entre la plus petite et la plus grande valeur de
y , intervient au carré dans l'expression du 
.
Il apparaît donc que
l'Anamorphose augmente le biais
présenté par la Méthode de
Moindres Carrés directe.
Il est d'ailleurs intéressant de superposer les droitespour
les c et d déduits par les diverses méthodes:
on observe que le "meilleur" ajustement s'éloigne
énormément de l'alignement initial (cf.
figure 7 ) .
Titre, résumé
retour: Varistance
Sommaire
suite:
chi-deux à 1 variable